Интегрирование заменой переменной (подстановкой)
Интегрирование подстановкой ( замена переменной ). Если функция f ( z ) определена и имеет первообразную при z 
Z , а функция z = g ( x ) имеет непрерывную производную при x X и её область значений g ( X ) Z , то функция F ( x ) = f [ g ( x )] × g' ( x ) имеет первообразную на Х и
F ( x ) dx = f [ g ( x )] • g' ( x ) dx = f ( z ) dz .
| П р и м е р . | Найти интеграл:  . |
| Р е ш е н и е. | Чтобы избавиться от квадратного корня, положим 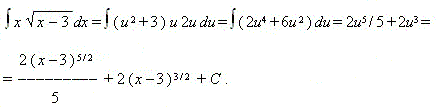 ,тогда x = u2 + 3 и, следовательно, dx = 2u du. Делая подстановку, имеем:  |
